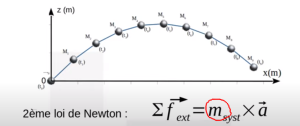
Justification scientifique des formules permettant l'équité
2ème loi newton appliquée à la course
Sur ce schéma la foulée est décrite comme la combinaison de 2 principes physiques tenant à la biomécanique et à la balistique .
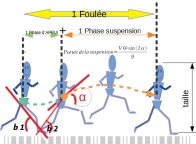
Principe de déplacement linéaire du centre de gravité dans la phase d'appui au sol représenté dans la première partie de la formule ci-dessous
Pour cet chaque type de course ou de saut, les angles de réception et de décollage jambe / centre de gravité sont définis grâce à l'étude des réalisations de sportifs de haut niveau .
L'avancée du centre de gravité est proportionnelle à la taille du coureur selon la formule :
(cos (angle amortissement)+cos(angle envol)) x Taille coureur/2
Dans l'exemple ci-dessous, nous avons estimé à 50° ces deux angles d'où la formule 2cos(b)*taille/2
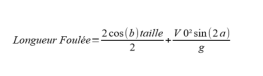
Principe de déplacement du centre de gravité d'un corps dans l'atmosphère se traduisant par la partie de formule V0²sin(2 angle envol cdg)/g
Démonstration physique du déplacement du centre de gravité lors de l'élévation lors de la foulée suite à la réaction du sol à la pression exercée par le coureur pour déformer la trajectoire
La portée de cette trajectoire du centre de gravité sera égale à V0² sin(2a) /g que nous retrouvons dans la deuxième partie de la formule .
Dans cette formule, la masse de l'individu est déterminante pour la portée de la trajectoire
Nous retiendrons que pour obtenir la même trajectoire d'élévation et la même portée un individu plus lourd aura une poussée proportionnellement plus importante à fournir lors de la phase d'élévation de la foulée.
voir la démo sur youtube :
https://www.youtube.com/watch?v=bItWh0ymx5o&t=5s